Introduction to Probability, Statistics and R

This book is due to be published in May, 2024. It is possible to order from Waterstones or foyles bookshops or Amazon.com or Amazon.co.uk in the UK.

The book is based on my lecture notes for many courses (modules), for example, Introduction to Probability and Statistics, taught to first and second year students in various BSc in Mathematics degree programmes.

Here is a preview pdf file. You may be able to access the book in various different formats through your own institution.

Key features of the book:

• This is an accessible textbook that engages the reader with many practical examples using probability and statistics for data science and machine learning.
• The book provides a comprehensive coverage of topics in probability, and both applied and mathematical statistics.
• The topics discussed in the book cover the syllabus for the 2023 Actuarial Statistics 1 examination administered by the Institute and Faculty of Actuaries in London.
• R, a popular statistical computing software package, is introduced from scratch and illustrated with many practical data sets. For example, see the R Getting Started page or the the package vignette.
• The book comes with its own dedicated R package ipsRdbs, available from CRAN. Once inside R and with the package installed, just asking for help for any data set included in the package will produce all the code required to reproduce the results and analysis presented in the book for that data set. Hence, a beginner reader can reproduce all those results without having to first learn all the commands and their exact syntax in R. This makes it seamless to learn, use and apply practical methods in introductory probability, statistics and beyond.
• The textbook also contains many theoretical and applied exercises for readers and instructors.

Some of the images below are shown using Creative Commons BY License detailed in the book.

• Chapter 1

  This chapter introduces basic statistics such as the mean, median and mode and standard deviation. It also provides introduction to many motivating data sets which are used as running examples throughout the book.

• Chapter 2

  This chapter introduces the R software package and discusses how to get started with many examples. It revisits some of the data sets already mentioned in Chapter 1 by drawing simple graphs and obtaining summary statistics.

• Chapter 3

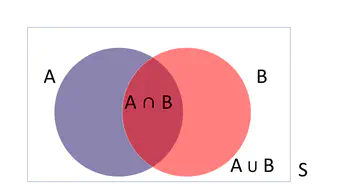
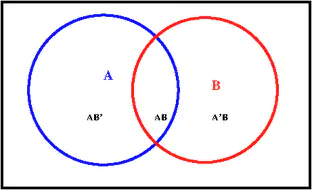
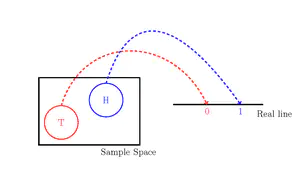
  The basic concepts of probability are introduced in this chapter. Elementary methods of counting, the number of permutations and the number of combinations are introduced and illustrated. Elementary methods for calculating probabilities are discussed and the general urn problem in probability is defined.

• Chapter 4

  This chapter introduces many advanced laws of probability such as the total probability theorem, conditional probability and the Bayes theorem. The famous Monty Python problem is discussed and illustrated using a simulation tool in R.

• Chapter 5

  Chapter 5 defines the random variables and their probability distributions. Many properties such as mean, variance, and quantiles of random variables are also defined here. Laws for expectations and variances of linear functions of random variables are also discussed.

• Chapter 6

  This chapter introduces the standard discrete distributions: Bernoulli, binomial, Poisson, geometric, hypergeometric and negative binomial. In each case the basic properties, such as mean and variance are obtained and the R commands to obtain probabilities and cumulative probabilities are illustrated.

• Chapter 7

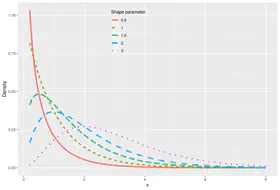
  This chapter introduces standard continuous distributions: exponential, normal, gamma and beta. As in Chapter 6, here we find the means and variances and also discuss the R commands for finding various quantities for each distribution.

• Chapter 8

  This chapter introduces the joint probability distribution for multiple random variables. It also discusses conditional and marginal distributions, conditional expectations, covariance and correlation. Finally it introduces the central limit theorem for the sum of independent random variables.

• Chapter 9

  This chapter introduces the basic concepts of statistical inference and statistical modelling. It distinguishes between population distributions and sample statistics (quantities). The concepts of estimators and their sampling (probability) distributions are also introduced.

• Chapter 10

  This chapter discusses three important methods for point estimation: method of moments, maximum likelihood and Bayesian methods.

• Chapter 11

  Chapter 11 discusses techniques such as the pivoting method for interval estimation. The central limit theorem is used to derive confidence intervals for the mean parameters of binomial, Poisson and normal distributions.

• Chapter 12

  Chapter 12 discusses testing of statistical hypotheses called null and alternative hypothesis. Definintions of many related keywords, e.g. critical region, types of errors while testing statistical hypothesis, power function, sensitivity and specificity are provided.

• Chapter 13

  Chapter 13 starts the Part III of this book on advanced distribution theory and probability. It discusses the moment generating function, cumulant generating function and probability generating function for discrete random variables.

• Chapter 14

  Chapter 14 is devoted to deriving distributions of transformed random variables in one and multiple dimensions. These techniques are used to derive sampling distributions of quantities of statstical interests while sampling from the normal distribution.

• Chapter 15

  Chapter 15 discusses bivariate and multivariate probability distributions. In particular, it discusses the marginal and conditional distributions associated with bivariate and multivariate normal distributions. It also discusses the joint moment generating function for the multivariate normal distribution.

• Chapter 16

  Chapter 16 discusses asymptotic theories which are often required to guarantee good properties of statistical inference techniques. Three types of modes of convergence in statistics are discussed and illustrated with the help of simulation using R routines.

• Chapter 17

  Chapter 17 kicks off Part V of the book on introduction to statistical modelling. It discusses the concepts related to simple regression modelling with many practical examples. The concepts of estimation, inference and predictions are discussed along with the required theoretical derivations.

• Chapter 18

  Chapter 18 generalises the simple regression techniques of the previous chapter to the case where there are multiple possible explanatory variables. This chapter describes the foundational basics for machine learning where the simple and multiple regression techniques are exploited heavily for practical problems.

• Chapter 19

  Finally, Chapter 19 introduces the concepts of analysis of variance which is a seen as a general model comparison technique where there are categorical explanatory variables. Theoretical generalisation of the techniques from the two preceding chapters are included and so are illustrations using R.

• Resources

  Further, resources (e.g. lecture slides) will be published through this page. Please revisit this page later. The data sets discussed in the book are published via the R package ipsRdbs available from CRAN.