Bayesian computation methods
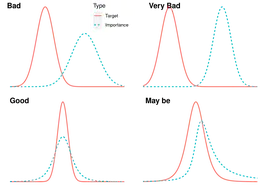
This chapter introduces the underlying concepts behind the powerful and popular computation methods used to make Bayesian inference for complex but parametric modeling problems. Presented with two simple running examples the chapter defines the methods of Monte Carlo, importance sampling, rejection sampling, Markov chain, Metropolis-Hastings algorithm, Gibbs sampler, Hamiltonian Monte Carlo and integrated nested Laplace approximation. These methods are illustrated using R commands in the bmstdr package and the results are compared with the exact theoretical and approximate results using numerical integration. The topics of Markov chain Monte Carlo (MCMC): convergence, diagnostics, run length and the number of chains are discussed from a practical implementation view point. Exact and MCMC estimated values of Bayesian model choice criteria such as the DIC and WAIC for a simple normal-normal example are compared. Exercises are provided to check understanding.
R code for reproducing the examples in Chapter 5.