Bayesian Modeling of Spatio-Temporal Data with R

BMSTDR book
BMSTDR book

BookAuthority Best Bayesian Statistics Books of All Time

Book Description

Applied sciences, both physical and social, such as atmospheric, biological, climate, demographic, economic, ecological, environmental, oceanic and political, routinely gather large volumes of spatial and spatio-temporal data in order to make wide ranging inference and prediction. Ideally such inferential tasks should be approached through modeling as modeling automatically aids in estimation of uncertainties in all conclusions drawn from such data. Unified Bayesian modeling, implemented through user friendly software packages, provides a crucial key to unlocking the full power of these methods for solving challenging practical problems.

Keeping the applied scientists in mind, this book presents most of the modeling with the help of R commands written in a purposefully developed R package to facilitate spatio-temporal modeling. However, the presentation in the book does not lose sight of mathematical and statistical rigor as it presents the underlying theories of Bayesian inference and computation in stand alone chapters in the first part which would be appealing to mathematics/statistics major final year undergraduate or post-graduate students who are in search of such modeling.

Key features of the book:

  • Accessible detailed discussion of a majority of all aspects of Bayesian methods and computations with worked examples, numerical illustrations and exercises with which the reader should be able to experience the methodologies live.
  • A spatial statistics jargon buster chapter that enables the reader to build up a vocabulary without getting clouded in modeling and technicalities in model fitting.
  • Computation and modeling illustrations are provided with the help of the dedicated R package bmstdr. The look and feel of the model fitting commands and their output resemble that of the lm command in R. A novice user, who is otherwise familiar with the lm command, will quickly be able to perform spatio-temporal modeling using well-known packages and platforms such rstan, INLA, spBayes, spTimer, spTDyn, CARBayes and CARBayesST.
  • Included are R code notes detailing the algorithms used to produce all the tables and figures. An online supplement presents the necessary data and the full code for reproducing these results.
  • Two dedicated chapters discuss practical examples of spatio-temporal modeling of point referenced and areal unit data. Taken from a variety of disciplines all illustrations are practical data driven rather than simulation based.
  • Throughout, the emphasis has been on validating models by splitting data into test and training sets following on the philosophy of machine learning and data science. The last chapter consolidates this connection formally by bringing in the Gaussian process based machine learning into the context of the topics presented in the book.

This book is designed to make spatio-temporal modeling and analysis accessible and understandable to a wide audience from bachelors, masters and PhD students to researchers, from mathematicians and statisticians to practitioners in applied sciences. By avoiding hard core mathematics and calculus, this book aims to be a bridge that removes the statistical knowledge gap from among the applied scientists.

empty_frame_LA_regions.png london_poverty.png maternfields.png met_adjusted_4thmax_99_05.png space_trend_longhurst.png temp_deep.png trend_wshed05-15_sd.png uscancer_rate.png v2_smr_england_07-11.png
  • Chapter 1

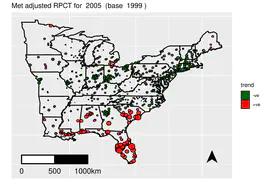
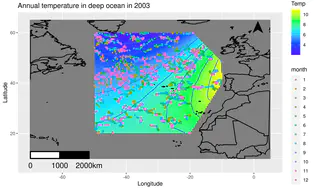
    Chapter 1 introduces the main data sets analyzed in this book. The example data sets are categorized in two broad types: point referenced data and areal unit data. The examples of the first type includes air pollution data from the state of New York, England and Wales and also a sub region in the Eastern United States east of the Mississippi river.

  • Chapter 2

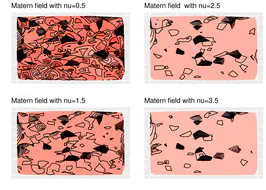
    This chapter introduces the main keywords and concepts we often encounter in spatial and spatio-temporal modeling. Written from a beginner reader’s point of view, it explains the basic concepts of stochastic processes, stationarity, variogram, isotropy, Matern covariance function, Gaussian Processes, space-time covariance function, Kriging, auto-correlation, Moran’s I and Geary’s C, internal and external standardization, spatial smoothers, CAR models and point processes.

  • Chapter 3

    This chapter emphasizes the need to carry out Exploratory Data Analysis (EDA) before embarking on any modeling endeavor. EDA techniques introduced include non-spatial techniques such as histogram, pairwise scatter plots; spatial methods such as variogram and Kriging; and temporal exploration such as time series plots.

  • Chapter 4

    Presented in a stand alone fashion, this chapter describes the main ideas of Bayesian inference needed in the rest of the book. Starting from the Bayes theorem in probability it discusses prior and posterior distributions, point and interval estimation, prior and posterior predictive distribution for model checking, hypothesis testing and Bayesian model choice statistics such as the Deviance Information Criteria (DIC) and Watanabe Information Criteria (WAIC).

  • Chapter 5

    This chapter introduces the underlying concepts behind the powerful and popular computation methods used to make Bayesian inference for complex but parametric modeling problems. Presented with two simple running examples the chapter defines the methods of Monte Carlo, importance sampling, rejection sampling, Markov chain, Metropolis-Hastings algorithm, Gibbs sampler, Hamiltonian Monte Carlo and integrated nested Laplace approximation.

  • Chapter 6

    This chapter introduces the general topic of practical Bayesian modeling and discusses its advantages over procedure based methods. The chapter discusses theoretical results for a simple linear regression model and also for a spatial model with known correlation parameter for point referenced data.

  • Chapter 7

    This is the main methodological chapter which discusses spatio-temporal modeling for point referenced continuous data. As in the preceding chapter it obtains exact theoretical results for a simple separable spatio-temporal model which serves as the base line for model comparison purposes.

  • Chapter 8

    This chapter showcases spatio-temporal modeling for point referenced data using five practical examples. The examples highlight the practical use of such modeling and extend the methodologies where necessary. The examples build on the basic concepts introduced in the earlier chapters, especially the previous chapter, on spatio-temporal modeling.

  • Chapter 9

    The topic of forecasting is discussed in this chapter. Several easy to use and scalable forecasting methods are presented for Gaussian data. The first of these is an exact Bayesian method based on the separable spatio-temporal model discussed in Chapter 7.

  • Chapter 10

    This chapter discusses Bayesian models for both areal and temporal areal data. As areal unit data are often discrete counts, this chapter first provides a gentle introduction to the generalized linear models (GLM).

  • Chapter 11

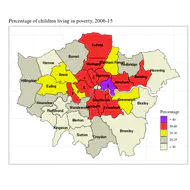
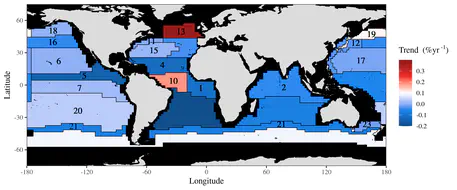
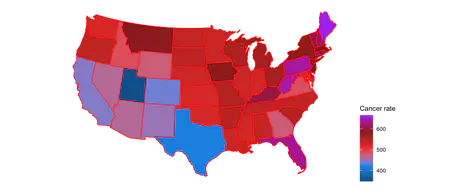
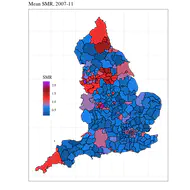
    Parallel to Chapter 8, this chapter showcases four examples of areal and temporal areal unit data sets. Click the links below to see the R-code for the examples. Assessing childhood vaccination coverage in Kenya Assessing trend in cancer rates in the USA Localized modeling of hospitalization data from England Assessing trend in child poverty in London All the model fitting is done using the Bcartime model fitting function in the bmstdr package.

  • Chapter 12

    This chapter aims to present GP based models for machine learning showing an immediate connection between the GP based regression models presented in the earlier chapters. The chapter highlights the equivalent correspondences between the different terminologies used in the fields of mainstream statistics and data science.

Last updated on Jun 28, 2024